2020年6月22日 講義用
PDF資料はこちら(終了から時間が経過したため、リンクを切っています。)
質問への回答
みなさま、感想・意見・質問などの送信、ありがとうございました。すべて読ませていただきました。こちらの伝えたいことを感じて頂けたことを知り、ほっとするとともに、もっとこうすればよかったなと反省もしています。
さて、いただいた質問について、こちらで順次回答をしていきます。順番に特に意味はありません。少しずつ更新していきますので、ご自身の質問への回答が得られるまで多少時間がかかるかもしれませんが、ご了承ください。
Q1. より質の高い論文を探すために、論文を検索する際に「原著論文」に絞るのはどうか。
A. はい。最終的には論文そのものをよく読むしかありませんが、原著論文に絞ることで効率はよくなると思います。特に、あまり質の高くないレビュー論文を対象から外せるというメリットがあります。その場合の注意点は以下の通りです。
- 原著論文の中にも「イマイチ」な論文は多くあります。論文誌によって、「原著論文」の定義が異なるからです。個人的には、きちんと査読がなされているものを「原著論文」と呼んでいますが、中には査読が行われていないもの(あるいは単に儀式として査読をやっているだけで、内容を伴わないもの)を「原著論文」と称している学術誌も見受けられます。
- 原著論文に絞ることで、有益なレビュー論文、症例報告が対象から落ちてしまうかもしれません。特に、質の高いレビュー論文(いわゆるシステマティックレビュー)は、研究上、非常に(×100)価値が高いです。文献検索をする際は、原著論文を探すだけでなく、(よい)レビュー論文を探すことも心がけてください。
Q2. ロジスティック回帰分析が使われた論文を目にすることも多いので、できれば改めて説明をしていたきたいです。
A. わかりました。そういうことでしたらぜひ!
ただ、文章で説明すると長くなってしまうので、動画を掲載します。関心のある方はご覧ください。恥ずかしいので、一定期間終了後削除します。
Q3. 一つ一つの検定方法について、よくわからないところがありました。もう一度説明していただけると嬉しいです。
A. お気持ちはわかるのですが、それを一つ一つ説明するとなるとちょっと大変です。テキストに指定されている『黒田裕子のStep by Step』のp148~p149を読んでみて、個別にどこがわからないかをご質問いただけるとありがたいです。
もし、別の本を、ということでしたら、中村好一先生の『基礎から学ぶ楽しい保健統計』がオススメです。中村先生のお人柄も出ていて、読むのが楽しい(特に脚注を読むのが好きです)本です。
それから、講義でもお話ししましたが、個々の検定について、説明を受けただけでわかるということはまずないと思います(よほど統計学的検定のセンスがある方なら別ですが、私も初めて統計学的検定について学んだときはちんぷんかんぷんでした。)。実際に使いながら、あるいは論文を読みながら学んでいくということになると思います。
そういう意味では次の質問で対応させてください。
Q4. 論文を読んでいてわからない統計学的検定があったら質問していいですか。
A. どうぞご質問ください。「この論文のここがわからない」や「この分析をしたいのだけれど」といった具体的な質問をいただけると、アドバイスがしやすいです。
メールアドレスでもTwitterのDMでもなんでも構いませんので、アクセスしてみてくださいませ。
※上記のURLは7月中で閉めてしまう予定です。
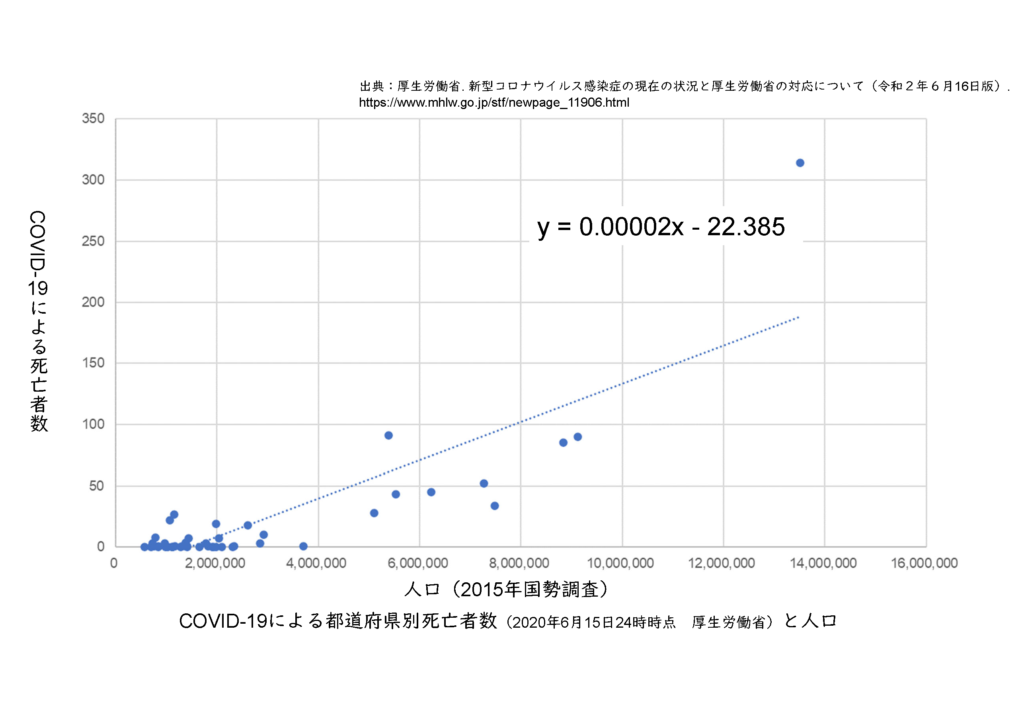
Q5. COVID-19による都道府県別死亡者数のグラフでyとxにあたる部分をもう一度教えてください。
A. yがCOVID-19による死亡者数(縦軸)、xが2015年国勢調査による人口(横軸)です。あくまで回帰分析の説明のために無理矢理作ったグラフなので、参考までに。。。
Q5. ある変数が正規分布に従うかどうかはどのように判断するのでしょうか。
A. 実はとても難しいです。保健医療福祉の分野で観察される事象については、完全な正規分布ということはまずないのです。このくらいだったら「正規分布に従うとみなす」といえるけれど、その絶対的な指標というのは存在しません。ある程度「えいやっ」と判断するしかないというのが実状です。
ではどう判断するかというと、まずはヒストグラムを書いてみてください。これが基本中の基本です。そして正規分布の山なりに近くなっているかどうかをみてください。
そして、更に詳しくみる場合はQ-Qプロットを書いたり、尖度・歪度といった指標をみたりします。一応、正規性の検定なんてのもあったりします。このあたりの説明は長くなるので、どうしても知りたい方は別途ご質問くださいませ。
Q6. 「成績」や「順位」は数値を扱うのに、質的変数の「順位尺度」に分類されるのはなぜでしょうか。
A. 実はとても回答が難しい質問です。いくつかに分けて説明します。
まず、順位尺度を質的変数に分類するか、量的変数に分類するか、というのは実は教科書によって違います。(少数派ですが)順位尺度を量的変数とみなすものもあります。
そこで、ここからは「数値を扱うのに、質的変数なのはなぜ?」という部分について解説します。実は少し誤解があります。
数値=量的変数、数値ではない=質的変数ではないのです。これは私の説明がよくなかったかもしれません。ここのところをよく理解して頂くために以下の例をみてみてください。「順序尺度」となっていますが、質問にある「順位尺度」と同じ意味です。
- 名義尺度(nominal scale) カルテなどの番号 11番、12番、13番(名前をつけただけ)
- 順序尺度(ordinal scale) 成績などの11位、12位、13位(順位をつけただけ)
- 間隔尺度(interval scale) 温度の11度、12度、13度(差に意味がある)
- 比尺度(ratio scale) お金の11円、12円、13円(原点の存在に意味がある)
出典:石村貞夫, デズモンド・アレン, 劉晨. 『すぐわかる統計学用語の基礎知識』2016; p124.
このように、同じ11,12,13でも異なる尺度になりえます。「数字で表せるかどうか」は尺度の分類において本質的な問題ではありません(むしろ誤解を生む可能性があります)。
名義尺度では、あくまで11番、12番という名前を付けただけであって、その数の大きさに意味があるかというとそうではありません。「あなたのカルテ番号とわたしのカルテ番号は214番分違うね」と言われたら、どう思いますか?「だからどしたん?」と聞きたくなりませんか?
それに対して、間隔尺度や比尺度では、数の大きさがとても重要です。「昨日より最高気温が10℃も上がるって!」といわれたら、「そりゃ体調に気をつけなきゃ」って思いますよね。あるいは「去年より10cmも背が伸びたよ!」といわれたら、「成長期やねぇ」と思いますよね。
※ちなみに間隔尺度と比尺度の違いは少し難しいです。0に意味があるかどうか、がその違いです。身長や体重には「0」があるので、比尺度です。「0」があるので、比で表すことができます。たとえば、60kgの人は50kgの人に対して1.2倍であると言えますが、「20℃は10℃の2倍である」という言い方は正確ではありません。札幌で昨日は-4℃だったのに、今日は4℃だ、という場合を考えて頂くと、「○℃は●℃の△倍である」という言い方が正確でないことがわかると思います。
一方、順序尺度では数値を使いますが、間隔尺度、比尺度とは大きく違います。順序は順序に意味があるのであって、順序の差、自体には大きな意味がないからです。
たとえば、マラソン大会で、あなたは120位でした。いつも競っている友人は110位でした。でも、二人の時間差は3秒でした(たまたま間に9人もいたんですね。大人数のマラソン大会ならよくあることです)。そうしたら、友人に「あんたと私は10番も違うんだよ!」と自慢されました。
どう思いますか?
「いやいや、たいして変わらんやん!」と思いませんか。
逆に、あなたは23位で、いつも競っている友人は24位でした。しかし、二人の時間差は2分ありました。そこで友人に「いやあ、1番しか違わなかったね!」と言われたらどう思うでしょうか。
「いやいや、2分も違うから!」と思いませんか。
このように順位の差は両者の本質的な差を表すとは限りません。この点が比尺度や間隔尺度と異なります。
※ただ、この話はなかなか難しい問題を孕みます。順番を大事にする人って世の中には多いですからね。。。
ということで、順序尺度でも(どころか名義尺度でも)数値を使います。しかし、だからといって比尺度や間隔尺度と同じ量的変数ということにはならないのです。
====
これでいただいたご質問へは回答できたと思います。「答えになっていない!」という声が聞こえてきそうですが。
途中にも書きましたが、こうして講義を担当し、その講義に皆さんが参加されたのも何かの縁です。ご質問などあれば、今後もぜひお寄せ下さい。できる限りサポートします。
(最終更新:2020年7月17日)